Merge Sort: A Friendly Guide for Students
Are you looking for a clear, step-by-step explanation of how Merge Sort works? You’re in the right place! Merge sort is one of the most elegant examples of the “divide-and-conquer” approach—an algorithm design technique that splits a problem into subproblems, solves them independently, and then combines the solutions. In this tutorial, we’ll walk through the main ideas behind merge sort, show you a concrete example, and provide a simplified diagram that traces each step in the process.
What Is Merge Sort?
Merge sort is a comparison-based sorting algorithm that:
- Divides the array into two halves.
- Conquers each half by recursively sorting them.
- Combines the two sorted halves into a single sorted array.
This strategy ensures that, as soon as each half is fully sorted, merging them is straightforward.
Why “Divide and Conquer”?
“Divide and conquer” is a powerful problem-solving method:
- Divide: Break the main problem into smaller subproblems.
- Conquer: Solve each of these subproblems (often recursively).
- Combine: Merge or join the subproblem solutions into the final answer.
When it comes to merge sort, the divide-and-conquer idea translates into splitting your array into two halves until each subarray has fewer than two elements (i.e., zero or one element). Subarrays of size 0 or 1 are already sorted, so those cases serve as the “base cases” of the recursion. Once we have these base cases, we merge these small sorted subarrays step by step until the entire array is sorted.
The Merge Sort Algorithm in Steps
- Base Case
If the subarray you’re looking at has fewer than two elements (i.e., p≥rp \geq rp≥r), it’s already sorted—do nothing. - Divide
Find the midpoint qqq between ppp and rrr. You can do: q=⌊p+r2⌋q = \lfloor \frac{p + r}{2} \rfloorq=⌊2p+r⌋ This splits your array into two subarrays:- Left subarray:
array[p..q] - Right subarray:
array[q+1..r]
- Left subarray:
- Conquer
Recursively sort both subarrays. Each subarray will go through the same divide-and-conquer process until it reaches the base case (size 0 or 1). - Combine (Merge)
Finally, merge the two sorted subarrays into a single sorted subarray. Merging is where most of the work happens, but it’s a straightforward process: repeatedly pick the smallest remaining element from the front of each subarray until you’ve exhausted both subarrays.
Walking Through an Example
Let’s see how merge sort works on a real example. Suppose we want to sort the array:
csharpCopy code[14, 7, 3, 12, 9, 11, 6, 2]
- Initial Array
p = 0r = 7- We have more than one element, so it’s not a base case.
- Compute midpoint: q=⌊(0+7)/2⌋=3q = \lfloor (0 + 7) / 2 \rfloor = 3q=⌊(0+7)/2⌋=3.
- This splits our array into:
- Left half:
[14, 7, 3, 12](positions 0..3) - Right half:
[9, 11, 6, 2](positions 4..7)
- Left half:
- Recursively Sort the Left Half (
[14, 7, 3, 12])- With
p = 0andr = 3, we again have more than one element. - Midpoint: q=⌊(0+3)/2⌋=1q = \lfloor (0 + 3) / 2 \rfloor = 1q=⌊(0+3)/2⌋=1.
- Left subarray:
[14, 7](positions 0..1) - Right subarray:
[3, 12](positions 2..3)
[14, 7]- p=0,r=1p = 0, r = 1p=0,r=1, midpoint q=0q = 0q=0.
- Sub-subarrays:
[14](position 0) and[7](position 1). Both have fewer than 2 elements, so each is sorted. - Merge them into
[7, 14].
[3, 12]- Single split gives
[3]and[12], each with just one element. - Merging produces
[3, 12].
[7, 14]and[3, 12]- Final result for the left half:
[3, 7, 12, 14].
- With
- Recursively Sort the Right Half (
[9, 11, 6, 2])- With
p = 4andr = 7, midpoint q=⌊(4+7)/2⌋=5q = \lfloor (4 + 7) / 2 \rfloor = 5q=⌊(4+7)/2⌋=5. - Left subarray:
[9, 11](positions 4..5) - Right subarray:
[6, 2](positions 6..7)
[9, 11]- Already in the correct order, but conceptually you still check the base cases.
- Result:
[9, 11].
[6, 2]- Split into
[6]and[2]. - Merge results in
[2, 6].
[9, 11]and[2, 6]- Final result for the right half:
[2, 6, 9, 11].
- With
- Combine (Merge) the Two Sorted Halves
- Left half sorted:
[3, 7, 12, 14] - Right half sorted:
[2, 6, 9, 11] - Merge them into: csharpCopy code
[2, 3, 6, 7, 9, 11, 12, 14]
- Left half sorted:
And that’s our sorted array!
Below is a simplified “top-down” view of merge sort’s divide-and-conquer on our example array. Each arrow shows how we split (divide) or merge the pieces. The diagram follows the same process described above, but in a more compact visual form.
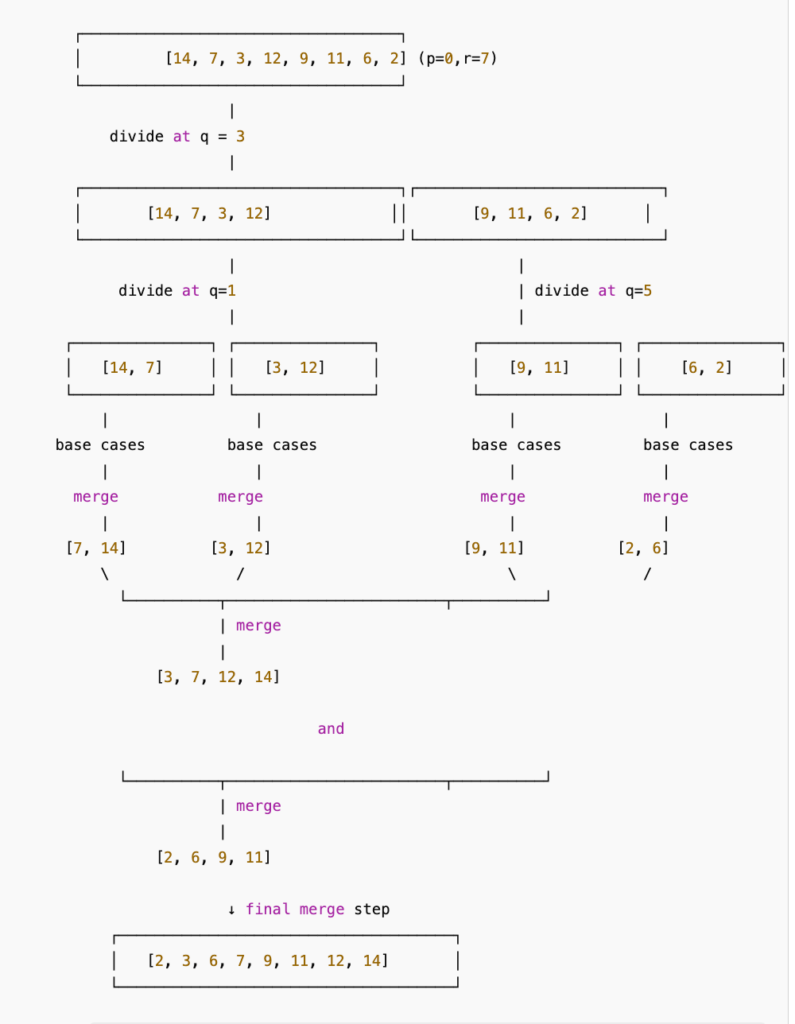
- We divide the array into two subarrays until each contains 0 or 1 elements (base cases).
- We conquer by sorting these tiny subarrays (which are already sorted by definition).
- We merge them step by step into larger, sorted subarrays until the entire array is sorted.
Key Takeaways
- Base Case: Subarray of length 0 or 1.
- Divide: Split the array around the midpoint.
- Conquer: Recursively sort the two smaller subarrays.
- Combine: Merge the sorted halves.
The heaviest lifting happens in the merge step, but because each subarray is already sorted, merging can be done in linear time (proportional to the total number of elements being merged). Overall, merge sort achieves O(nlogn)O(n \log n)O(nlogn) performance in the average and worst cases, making it a reliable go-to sorting method for many applications.
Next Steps
If you’ve followed along successfully, you now have a solid understanding of how merge sort works. In future lessons, we’ll dive deeper into:
- How to implement the “merge” step efficiently.
- Complexity analysis (why merge sort is O(nlogn)O(n \log n)O(nlogn)).
- Comparing merge sort with quick sort, insertion sort, and other algorithms.
Keep practicing, and you’ll be able to implement merge sort (and other divide-and-conquer algorithms) with confidence. If you have any questions, feel free to reach out or explore our other resources on sorting, searching, and beyond!
